Aquí les dejo la tarea de la LEY DE OHM tomar en cuenta que algunos de estos ejercicios constan en la prueba.

FÍSICO-QUÍMICA: 2DO BACHILLERATO C, D

FÍSICO-QUÍMICA

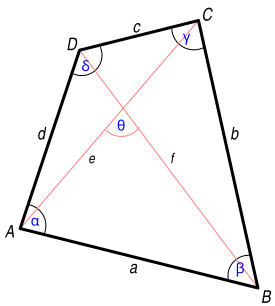
LA TENSIÓN EN BORNES de salida de un generador eléctrico cuando entrega una corriente de intensidad I a una resistencia de Carga R, es igual a la fuerza electromotriz E  menos la caída de tensión, que tiene lugar en la propia resistencia interna del generador r.

1. Cuando entrega corriente ( descarga)

    Tensión en bornes = fem - caída de tensión de resistencia interna = E -r I

2. Cuando recibe corriente ( carga )

    Tensión en bornes = fem + caída de tensión de Resistencia interna = E + r I

        I = E

             r + R

PROBLEMAS DE LA LEY DE OHM

1.- Por la sección transversal de un alambre pasan 10 coulumbios en 4 segundos. Calcular la intensidad de la corriente eléctrica.

2.- La intensidad de la corriente que atraviesa a un conductor es de 5 A. Calcular la carga que pasa por su sección transversal en 2 seg.

3.- Un conductor tiene una resistencia de 4 ohmios. Calcular la diferencia de potencial en sus extremos cuando le atraviesa una intensidad de 2 A.

4.- En los extremos de un conductor hay una diferencia de potencial de 20 voltios, cuando le atraviesa una corriente de 4 A. Calcular la resistencia.

5.- Un conductor está atravesado por una corriente de 5 A y esta corriente efectúa un trabajo de 500 joules en 10 seg. Calcular la diferencia de potencial en los extremos del conductor.

6.- Una batería de 10 V y 1 ohm de resistencia interna se conecta a una resistencia de carga R = 4 ohmios. Hallar: a) La intensidad de la corriente en el circuito. b) La caída de tensión en la resistencia interna y en la carga.

7.- Una pila seca tiene una fem de 1,52 V. Hallar la resistencia interna r si la corriente de cortocircuito vale 25 A.

8.- Una pila tiene una fem de 1,54 V. Al conectarla una resistencia de 1 ohmio, un voltímetro entre los bornes de la pila indica 1,40 V. Hallar su resistencia interna.

9.- Hallar la d.d.p. para que por una una resistencia de 28 ohmios circule una corriente de 3 A.

10.- Una bobina de 5 ohmios de resistencia en serie con una bombilla se conecta a una fuente de tensión de 110 V. Hallar la resistencia de la lámpara sabiendo que la corriente en el circuito es de 4 A.

LIC. Sonia López

Un cuadrilátero es un polígono que tiene cuatro lados. Los cuadriláteros pueden tener distintas formas, pero todos ellos tienen cuatro vértices y dos diagonales, y la suma de sus ángulos internos siempre da como resultado 360º.
Por lógica todos los cuadriláteros son cuadrángulos, ya que esta definición se aplica a los polígonos de cuatro ángulos.

Elementos de un cuadrilátero

Los componentes de un cuadrilátero son los siguientes:

• 4 vértices: puntos de intersección de los lados que conforman el cuadrilátero.
• 4 lados: segmentos limitados por dos vértices contiguos.
• 2 diagonales: segmentos cuyos extremos son dos vértices no contiguos.
• 4 ángulos interiores: conformados por dos lados y un vértice común.
• 4 ángulos exteriores: prolongación de los lados.

Clasificación de los cuadriláteros

Deltoides.

Los cuadriláteros se clasifican según el paralelismo de sus lados:

1. Paralelogramos: sus lados opuestos son paralelos
   1. 1. Cuadrado
      2. Rombo
      3. Rectángulo
   2. Oblicuángulos
2. Trapecios: dos lados paralelos; los otros dos, no
   1. Trapecio rectángulo
   2. Trapecio isósceles
   3. Trapecio escaleno
3. Trapezoide: lados no paralelos
   1. Trapezoide simétrico o deltoide
   2. Trapezoide asimétrico

Taxonomía de los cuadriláteros

En el gráfico ilustrativo de la taxonomía de los cuadriláteros se pasa de las definiciones más generales a las más específicas siguiendo el sentido de las flechas.
Así se parte de un cuadrilátero definido como un polígono cerrado de cuatro lados, sin más restricciones, para diferenciar los cuadriláteros compuestos de los simples.
En un cuadrilátero complejo, dos de sus lados se cortan. En uno simple los lados no se cruzan.
Los cuadriláteros simples se dividen en:

• Cóncavos. En un cuadrilátero cóncavo al menos uno de sus ángulos interiores mide más de 180º.
• Convexos. Un cuadrilátero convexo no tiene ángulos interiores que midan más de 180º. Los convexos se subdividen en:

1. Cuadrilátero cíclico, si se puede trazar una circunferencia que pase por sus vértices.
2. Cuadrilátero tangencial, si se puede trazar una circunferencia tangente a cada uno de sus lados.
3. Trapecios, si tienen dos lados paralelos. Se diferencian:
   1. Romboide, como caso más general de paralelogramo, si los lados son paralelos dos a dos.
   2. Trapecio rectángulo, que tiene un lado perpendicular a sus bases.
   3. Trapecio isósceles, cuyos lados no paralelos son de igual medida. Este trapecio también es cíclico.

A un cuadrilátero que al mismo tiempo sea cíclico y tangencial se le denomina cuadrilátero bicéntrico. El deltoide es tangencial con dos pares de lados iguales.
Un caso particular de trapecio isósceles es cuando la longitud de una de las bases es igual que la de sus lados, por lo cual se configura un trapecio de tres lados iguales.
El rectángulo es un cuadrilátero que simultáneamente cumple las características de:

• Paralelogramo, al ser paralelos sus lados opuestos.
• Trapecio rectángulo, porque los lados son perpendiculares a las bases.
• Trapecio isósceles, por ser de igual longitud los lados que no constituyen las bases.

Del mismo modo se puede verificar que el rombo es un deltoide paralelogramo, pues cumple las características de ambos.
Por último, el cuadrado puede considerarse rombo, rectángulo, con lados iguales y bicéntrico.

Fórmulas

Los cuatro lados de un cuadrilátero: a, b, c, d ;
los cuatro vértices: A, B, C, D ;
las dos diagonales: e, f.

• La suma de los ángulos internos es igual a 360°:

• Si las diagonales son perpendiculares, ocurre la relación siguiente:

• El área de un cuadrilátero se puede calcular mediante cualquiera de estas seis fórmulas: